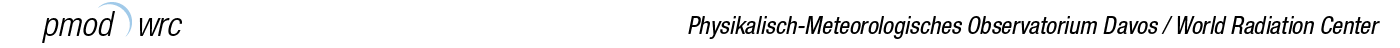Introduction
Solar irradiance is the fundamental driver of all climate processes on Earth. Past climate changes can be related to variations in TSI while human activity has had an increasing effect on Earth’s climate over the past ~150 years. High-accuracy TSI measurements help to assess solar forcing on global temperatures in order to distinguish between anthropogenic and natural climate change. TSI has been continuously measured in space since the late 1970’s, and towards the end of the 1990’s, the scatter between different radiometers decreased. The current best estimate of TSI is ~1361 W.m-2.
Results and Discussion
The description of the procedures used to construct the composite from the original data shown in Figure 1 (upper panel) can be found in Fröhlich and Lean (1998) and Fröhlich (2000). Radiometrically it is based on the ACRIM-I and II records; before the start of the ACRIM-I measurements in 1980, during the spin mode of SMM, and during the gap between ACRIM-I and II, corrected HF data are inserted by shifting the level to fit the corresponding ACRIM data over an overlapping period of 250 days on each side into the ACRIM sets. In early 1996, the VIRGO data take over, again shifted to agree with ACRIM-II. Finally the composite record is adjusted via ACRIM-II to SARR (Space Absolute Radiometer Reference) which was introduced by Crommelynck et al. (1995) and allows the comparison of different space experiments (done in spring 1993). The data fromERBE and ACRIM-III, as well as an empirical model, are used for comparisons and for internal consistency checks. It is important to note that the model is an independent source of information for comparisons and as long as it is not used over solar cycle time scales it provides a reliable time-series for time scales of less than a year. So it will be used in all comparisons as it is available as a daily record which is important for the interpolation between ERBE data with their 14-day sampling.
The most important issues for the construction of the composite are:
- Correction of the early HF measurements from NIMBUS 7 to account for its early increase, degradation and non-exposure dependent increase (Fröhlich and Lean, 1998; Fröhlich, 2006).
- Assessment of the early increase and degradation of ACRIM-I (Fröhlich, 2006).
- Tracking of ACRIM-II to ACRIM-I by comparison with only HF, corrected as described in the first bullet (earlier versions also used ERBS and the model, see Fröhlich (2000) and Fröhlich (2003)).
- Detailed assessment of the influence of the many operational interruptions in the ACRIM-II record (Fröhlich, 2004).
The related problems are now discussed in greater as well as in corresponding references (mainly in ISSI WS2005). The analysis of the PMO6V radiometer of the VIRGO experiment on SOHO allowed not only a model for the changes to be developed, but also to differentiate between effects of quite different origin. From our experience with the radiometer series for SOVIM, an experiment flown within SOLAR on the International Space Station (until October 2012), and by re-examination of the retrieved radiometers from EURECA, we learned that the early increase is due to a change in absorption of the primary aperture and its influence on the sensitivity by extra IR radiation and straylight from the baffle. So, it became clear, that this influence may be important for all radiometers used in space missions, which have their primary aperture directly in front of the cavity. And, indeed it could be detected in ACRIM-I with similar amplitudes as observed for the PMO6V radiometers of VIRGO. Moreover, tests at TRF of LASP confirmed the large influence on spares of PMO6V and ACRIM-3, which also explains the difference in absolute scale between these classical radiometers and TIM/SORCE of several tenths of a percent. So the early increase is a change of this effect due a change of the reflectivity of the primary aperture. In a next step degradation, ACRIM-I has to be modelled again. This is quite straight forward as the model developed for the PMO6V radiometers which takes the dose into account, works very well. It is only complicated by the fact that during the spin-mode operation of SMM (after failure of the pointing system of SMM in late 1980 until repair in 1984) the exposure was drastically reduced, which, however, can be taken into account accordingly.
The situation for the HF radiometer is more complicated as there is no back-up instrument which can be used for in-flight exposure dependent corrections. So we need a reference for the early observations, which is built from the proxy model calibrated with corrected ACRIM-I (over the period 1980-1985) and used to extrapolate ACRIM-I back to November 1978, the start of NIMBUS-7. Moreover, ERBS data are used as a reference after ACRIM-I was terminated. Another complication is the fact that the time-series has many slips which are mainly due to changes in the orientation of the spacecraft and due to switch-off, which have not been taken into account in the original evaluation. In contrast to the earlier analysis, we determine the HF sensitivity changes over its full period and the trend no longer needs to be determined during the ACRIM gap by comparison with ERBS and the proxy model as in Fröhlich (2000). The final result of the corrected HF data set is not fundamentally different from what was determined earlier with a much simpler and more subjective method, but the corrections are now internally consistent and completed over the full HF measurement period at once. It is interesting to note that there is also an increase in sensitivity which is not exposure dependent, similar to the effect on DIARAD/VIRGO (see also the discussion of the VIRGO TSI data: VIRGO_TSI-vers64.pdf). The magnitude of the correction demonstrates how important they are (up to 1 W.m-2).
Figure 1. Comparison of the PMOD composite with original data sets. Smooth full lines indicate that the radiometer is the basis for the composite and if coincident with zero that no corrections other than an overall shift has been applied. If an instrument is not used, the color of the line is dimmed. The HF record needed the most important corrections mainly for the long-term changes. The ACRIM-I record in 1980 is also changed to take the early increase and a revised version of the degradation algorithms into account. Results from ERBE, DIARAD/VIRGO (evaluated with the IRMB algorithm) and TIM/SORCE are plotted as dotted lines.
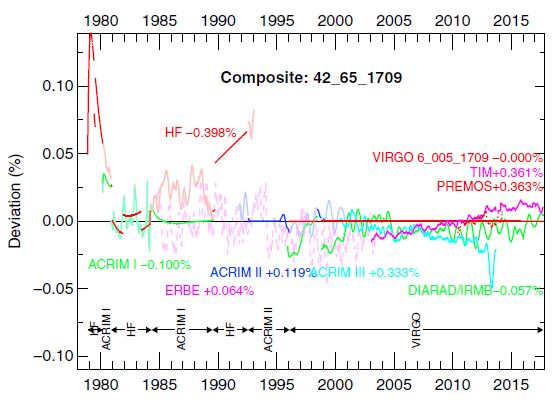
Figure 2. Comparison of the PMOD composite with the two other composites. The PMOD composite is on the original scale of VIRGO in this plot.
With these corrections, we are now ready to reference ACRIM-II to ACRIM-I. This is done by a weighted average of the ratios of ACRIM-I to the corrected HF and ERBS data and the corresponding average ratios of ACRIM-II. With the new treatment of the HF correction, this radiometer is now independent of ERBS, a further improvement over the earlier analysis. Having done this scaling, the rest is straightforward and consists of adjusting the HF and the ACRIMs to VIRGO. The comparison to the original data is shown in Figure 1 where the major corrections are obvious: early HF, ACRIM-I during 1980, HF during the ACRIM gap.
The final PMOD-composite is shown Figure 2 together with the ACRIM and IRMB composites. The result of a more detailed comparison of the three composites with ERBE is presented in Figure 3. After the detection of the early increase in the ACRIM-I data set and due to the fact that the ERBS radiometers are copies of ACRIM-II (manufactured by TRW for NASA Langley) and assuming that both have the same type and geometry of apertures, they should behave very similarly for the early increase. As the total exposure time is less than 3 days, only a correction for the earliest increase has to be applied.
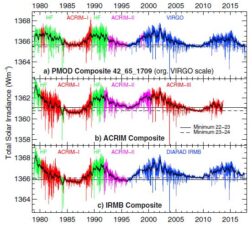
Figure 3. Comparison of the PMOD, ACRIM and IRMB composites with ERBE. The result illustrates the jump of the ACRIM composite over the ACRIM gap which corresponds to the corrections to the HF radiometer applied for the construction of the PMOD composite. The observed upward trend as seen in Figure 2 has been corrected with the early increase coefficients of ACRIM-I and the dose seen by ERBE as descibed in Fröhlich (2006). This graph also illustrates quite impressively how different the results of DIARAD/VIRGO are when evaluated with the IRMB algorithm. The fit with an exponential function which also takes a change over the SOHO-vacation gap into account, independently confirms the non- exposure dependent changes, that the VIRGO team determined and applied. Fortunately, DIARAD and possibly HF are the only radiometers for which such an effect has been identified. Without comparison with some other independent instruments there is no way to assess such changes. This was also the reason that VIRGO had two different types of radiometer.
An estimate of the uncertainty of the long-term behaviour of the composite TSI can be deduced from the uncertainty of the slope relative to ERBE. For the PMOD composite the slope over the whole period amounts s to 1.1 ± 2.1 ppm/year. Although this standard deviation is partly determined by the sampling of ERBE we may estimate the uncertainty of a possible trend to be <3 ppm/year for periods longer than 10 to 15 years. This implies a possible change of 50 to 80 ppm over the 23 years of the observations. If we add the uncertainties related to the tracing of ACRIM-II to I and of the HF correction (60 ppm), a total uncertainty of 92 ppm is obtained. The observed change of the PMOD composite as the difference between two successive minima amounts to -10 ppm which is not significantly different from zero at the 3-sigma level.
The comparison of the three composites with ERBE shows that the PMOD composite is the most consistent. So, if one believes the ERBE record, and with the Spearman’s rank correlation coefficient s of the PMOD, ACRIM and IRMB composites of 0.751, 0.678 and 0.695, respectively, it becomes clear which one should be chosen as a reliable estimate of the total solar irradiance for the last three solar cycles.
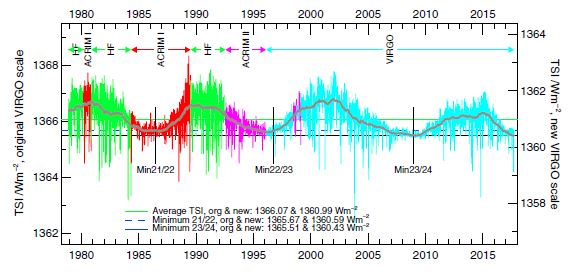
Figure 4. The PMOD composite TSI as daily values plotted in different colors for the different originating experiments. The new absolute scale of VIRGO is indicated on the right while the values of the average and minimum values are shown on both scales.
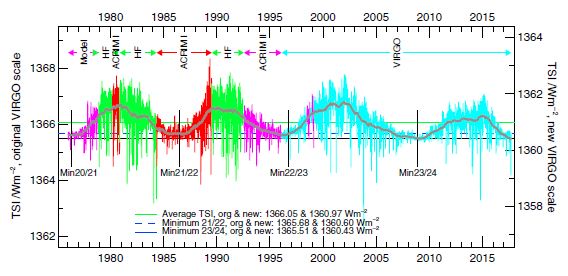
Figure 5. The extended PMOD composite TSI as daily values plotted in different colors for the different experiments. Differences between solar minima and amplitudes of the three cycles are also shown.
Through the success of the proxy model (e.g. described in Fröhlich and Lean, 2004) in explaining both the short and long-term behaviour of the Sun during the last three cycles, it is now possible to expand the composite back to the solar minimum in 1976 (Figure 5).
The TSI composite is referenced to the VIRGO rather than the SARR scale since version 4.2. The new characterisation of the VIRGO radiometer (see VIRGO_Char2Space) provides a new absolute scale which is about 5.8 W.m-2 or 0.42% lower than the original scale. Both scales are presented in Figures 4 and 5 as well as in the data files (composite here, and extended here). During the last solar minimum, TSI from VIRGO was 1359.66 ± 2.47 W.m-2 which is within less than half the uncertainty equal to that from TIM at 1360.52 W.m-2.
References
Crommelynck, D., A. Fichot, R. B. Lee III, and J. Romero, (1995), First realisation of the space absolute radiometric reference (SARR) during the ATLAS 2 flight period, Adv. Space Res., 16, 17-23.
Dewitte, S, D. Crommelynck, S. Mekaoui, A. Joukoff, (2004), Measurement and Uncertainty of the long-term Total Solar Irradiance Trend, Sol. Phys., 224, 209-216.
Fröhlich, C., and J. Lean, (1998), The Sun’s total irradiance: Cycles and trends in the past two decades and associated climate change uncertainties, Geophys. Res. Lett., 25, 4377-4380.
Fröhlich, C., (2000), Observations of irradiance variability, Space Science Reviews, 94, 15-24.
Fröhlich, C., (2003), Long-term behaviour of space radiometers, Metrologia, 40, 60-65.
Fröhlich, C., (2004), Solar Irradiance Variability, in Solar Variability and its Effect on climate, Chapter 2: Solar Energy Flux Variations, AGU, Geophysical Monograph Series No. 141, 97-110.
Fröhlich, C. and J. Lean, (2004), Solar Radiative Output and its Variability: Evidence and Mechanisms, Astron. and Astrophys. Rev., 12, pp. 273-320, doi: 10.1007/s00159-004-0024-1
Fröhlich, C., (2006), Solar Irradiance Variability Since 1978: Revision of the {PMOD} Composite During Solar Cycle 21, Space Sci. Rev., 125, 53-65, doi: 10.1007/s11214-006-9046-5
Fröhlich, C., (2012), Total solar irradiance observations, Surveys in Geophysics, 33, 453-473, doi: 10.1007/s10712-011-9168-5
Willson, R. C., (1997), Total solar irradiance trend during solar cycles 21 and 22, Science, 277, 1963-1965.
Willson, R. C., and A. V. Mordinov, (2003), Secular total solar irradiance trend during solar cycles 21 and 22, Geophys. Res. Lett., 30, 1199-1202.